GRÁFICOS DE CONTROL
1. WALTER SHEWHART GRÁFICOS DE CONTROL
Los gráficos de control o el Control Estadístico de Procesos (SPC) es un campo que se remonta a la década de 1920. El Dr. Walter A. Shewhart un físico, ingeniero y estadístico estadounidense, conocido como el padre del control estadístico de la calidad de Bell Telephone Laboratories fue uno de los primeros en trabajar en este campo. En 1924 escribió un memorando que mostraba un gráfico de control moderno, una de las herramientas básicas del SPC.
La Segunda Guerra Mundial vio la introducción generalizada de este y otros métodos en la industria estadounidense y fueron clave para la victoria de los aliados.
Ahora el SPC es parte de las core tools de la Automotive Industry Action Group” (AIAG) desarrolladas para diseñar, desarrollar, medir, controlar, registrar, analizar y aprobar productos y servicios de calidad que satisfagan las necesidades y expectativas del cliente.
2. ¿QUÉ SON LOS GRÁFICOS DE CONTROL?
Inspeccionar la calidad de un producto al final del proceso es muy caro; el producto debe fabricarse bien a la primera. Por lo tanto, el proceso de fabricación debe ser estable y repetible y capaz de operar con poca variabilidad alrededor de la dimensión nominal o objetivo.
El Control Estadístico de Procesos (SPC) es una herramienta poderosa para lograr la estabilidad del proceso y mejorar la capacidad mediante la reducción de la variabilidad.
Así pues podemos decir que el control estadístico de proceso es una herramienta para la mejora y se debe usar en conjunto con otras herramientas como lo son: Histogramas, Gráficos de Pareto, diagramas causa efecto, diagramas de dispersión, hojas de verificación, amef de proceso, análisis de sistemas de medición y planes de control.
3. VARIACIÓN: CAUSAS COMUNES Y ESPECIALES
No existen dos productos o características que sean exactamente iguales, debido a que cualquier proceso contiene muchas Fuentes de Variabilidad. Las diferencias entre productos pueden ser grandes, o estas pueden ser dimensionalmente pequeñas, pero siempre están presentes.
Para administrar cualquier proceso o reducir la variación, dicha variación debería ser rastreada hacia sus fuentes. El primer paso es distinguir entre causas de Variación Comunes y Especiales.
3.1 Causas Comunes
En cualquier proceso de producción, independientemente de lo bien diseñado o cuidadosamente mantenido que esté, siempre existirá cierta cantidad de variabilidad inherente o natural,esta variabilidad natural o «ruido de fondo» es el efecto acumulativo de muchas causas pequeñas, esencialmente inevitables.
Cuando el ruido de fondo en un proceso es relativamente pequeño, generalmente se considera que se encuentra a un nivel aceptable de desempeño.
Se dice que un proceso que está operando con solo causas de variación fortuitas (causas comunes) está bajo control estadístico ya que las causas fortuitas son una parte inherente del proceso.
3.2 Causas Especiales
Ocasionalmente, pueden estar presentes otros tipos de variabilidad en el resultado de un proceso, esta variabilidad se puede deber generalmente a errores humanos, de máquina o de materias primas, esta variabilidad por lo regular es grande en comparación con la variabilidad inherente al proceso.
Nos referimos a estas fuentes de variabilidad que no forman parte del patrón de ruido de fondo como causas asignables o causas especiales.
Se dice que un proceso que está operando en presencia de causas asignables está fuera de control.
A menos que todas las Causas Especiales de Variación se identifiquen y se actúe sobre ellas, estas pueden continuar afectando los resultados del proceso en formas impredecibles
Las Causas Especiales son señalizadas por uno o más puntos fuera de los Límites de Control o por patrones no aleatorios de puntos dentro de los Límites de Control.
Como se puede observar existe una estrecha conexión entre los gráficos de control y las pruebas de hipótesis. Básicamente, el gráfico de control está ejecutando una prueba de hipótesis en cada punto graficado de que el proceso se encuentra en un estado de control estadístico o no lo está.
Un de los puntos dentro de los límites de control equivale a no rechazar la hipótesis de control estadístico H0, y uno de los puntos fuera de los límites de control equivale a rechazar la hipótesis nula de que el proceso se encuentra en control estadístico.
4. PARA QUÉ SIRVEN LOS GRAFICOS DE CONTROL
Los Gráficos de Control nos sirven especialmente para mejorar los procesos y en general debemos observar lo siguiente:
- La mayoría de los procesos no operan en un estado de control estadístico.
- En consecuencia, el uso rutinario y atento de los gráficos de control identificará las causas asignables. Al eliminarse estas causas asignables del proceso, se reducirá la variabilidad y se mejorará el proceso.
- El gráfico de control sólo detecta causas asignables, la organización deberá actuar para encontrarlas y eliminarlas.
- Un plan de acción para responder a las señales de alarma del gráfico de control es vital.
4.1 Los gráficos de control son una técnica probada para mejorar la productividad ya que reducirán el desperdicio y el retrabajo, que son los principales factores que destruyen la productividad en las empresas. Si se reduce el desperdicio y el reproceso, la productividad aumenta, los costos disminuyen y la capacidad de producción (medida en el número de piezas buenas por hora) aumenta.
4.2 Los gráficos de control son eficaces en la prevención de defectos. El gráfico de control ayuda a mantener el proceso bajo control, lo que es coherente con la filosofía de «hacerlo bien a la primera». Nunca será más barato separar las unidades «buenas» de las «malas» y luego re-trabajarlas que hacerlas bien desde el principio. Si no se cuenta con un control de proceso efectivo, usted le está pagando a alguien para que re-trabaje un producto no conforme.
4.3 Los gráficos de control evitan ajustes de proceso innecesarios. Un gráfico de control puede distinguir entre ruido de fondo y variación anormal; ningún otro dispositivo, incluido un operador humano, es tan eficaz para hacer esta distinción. Si los operadores del proceso ajustan el proceso basándose en pruebas periódicas no relacionadas con un programa de gráficos de control, a menudo reaccionan de forma exagerada al ruido de fondo y realizan ajustes innecesarios. Estos ajustes innecesarios pueden provocar un deterioro del rendimiento del proceso. En otras palabras, el gráfico de control es coherente con la filosofía de «si no está roto, no lo arregle».
4.4 Los gráficos de control proporcionan información de diagnóstico. Con frecuencia, el patrón de puntos en la tabla de control contiene información de valor diagnóstico para un operador o ingeniero experimentado. Esta información permite al operador implementar un cambio en el proceso que mejorará su desempeño.
4.5 Los gráficos de control proporcionan información sobre la capacidad del proceso. El gráfico de control proporciona información sobre el valor de los parámetros importantes del proceso y su estabilidad en el tiempo. Esto permite realizar una estimación de la capacidad del proceso. Esta información es de gran utilidad para los diseñadores de productos y procesos.
Los gráficos de control se encuentran entre las herramientas de control de gestión más efectivas y son tan importantes como los controles de costos y los controles de materiales. La tecnología informática moderna ha facilitado la implementación de gráficos de control en cualquier tipo de proceso, ya que la recopilación y el análisis de datos se pueden realizar en una computadora PC o en una terminal de red de área local en tiempo real.
5. COMO HACER GRAFICOS DE CONTROL
Vamos a trabajar con los gráficos de control clásicos, estos gráficos de control fueron propuestos por primera vez por el Dr. Walter A. Shewhart, y los gráficos de control desarrollados de acuerdo con estos principios a menudo se denominan gráficos de control de tipo Shewhart.
El modelo es sencillo, debemos primero determinar la variable crítica de proceso queremos monitorear.
Luego debemos verificar que nuestra variable aleatoria cumpla con un comportamiento independiente y provenga de una distribución normal o muy aproximada a una distribución normal.
En caso de no cumplir con el supuesto de normalidad te recomendamos obtener este bono gratuito (box cox y teorema del límite central) si quieres saber como hacer una prueba de independencia en minitab por favor ve a esta liga (prueba de independencia)
Calculamos la media y la desviación estándar de la variable, donde la media es la línea central, el límite de control superior y el límite de control inferior se convierten en la “distancia” de los límites de control desde la línea central, expresada en unidades de desviación estándar, por lo general utilizamos 3k o tres desviaciones estándar lo cual nos garantiza que el 99 % de los valores en estado estable deben caer dentro de estos límites.
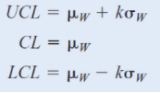
Para ver un ejemplo de cómo construir un gráfico de control en excel por favor ve a esta liga que te mostrara el caso de un gráfico continuo y rango medio (I-RM) grafico excel
6. TIPOS DE GRÁFICOS DE CONTROL
6.1 Gráficos de control datos continuos
6.1.1 Gráficos de control x-r
Gráficas de Control basadas en datos continuos cuyas características son las siguientes:
Son usados para variables continua (por ejemplo un diámetro expresado en cm) y tenemos la posibilidad de sacar una muestra que puede ir de 2 a 9 piezas, hay que considerar que los datos deben ser normales e independientes además de seleccionar subgrupos o muestras racionales que permitan excluir causas especiales dentro de cada subgrupo.
ver una explicación de la importancia de subgrupos racionales
Si un punto cae fuera de los límites de control es posible que el proceso ya no sea estable, e igual sucede en el caso de la gráfica R (rangos) que es la que monitorea la estabilidad de la variabilidad del proceso.
descargue un ejemplo de una gráfica x-r en excel
6.1.2 Gráficos de control x-s
Es básicamente lo mismo que la gráfica x-r solo que en lugar de graficar el rango de cada subgrupo lo que estaríamos graficando es la desviación estándar del subgrupo.
La gráfica x-r es más común por su sencillez en los cálculos, pero ahora con los paquetes computacionales es más sencillo elaborar un gráfico x-s, sin embargo hay que notar que las mismas alarmas dará una y la otra, esto es no hay diferencia entre ellas en lo que respecta a su utilidad y depende los deseos de cada analista cual se adapta más a sus necesidades.
descargue un ejemplo de una gráfica x-s en excel
6.1.3 Gráficos de medianas y rangos
Es una variante de los gráficos x-r, solo que en este caso los promedios de los subgrupos no pueden ser calculados en forma conveniente o resulta más fácil para el usuario calcular la mediana, de este modo utilizar esta gráfica para monitorear el proceso es más atractivo desde el punto de vista del usuario.
Las alarmas que arroja el gráfico y la efectividad de la misma para monitorear la estabilidad del proceso es como ya se dijo similar a la x-r.
Descargue un ejemplo de una gráfica Mediana – Rango en excel
6.1.4 Gráficos de control individuales
Gráficas de Lecturas Individuales y Rangos Móviles (I,MR) para datos continuos individuales; es un gráfico que es utilizado cuando no tenemos la oportunidad de sacar una muestra de tamaño n de la población en el tiempo t. El proceso solo nos permite tener un solo dato en el tiempo t.
Ejemplos de esta situación son procesos homogéneos por naturaleza como en los procesos continuos de elaboración de materias primas, ejemplo la fabricación de cemento, aluminio, pintura entre otros.
Ya que tenemos un solo dato en el tiempo (I), nos podremos ver perjudicados por la distribución de la población de la que provienen nuestros datos, la cual podría no ser normal, cosa que evitamos en las gráficas x-r en las cuales podíamos tener un grupo de tamaño n el cual nos permite hacer uso del teorema de límite central y con eso conseguir la normalidad de la distribución de los datos.
Descargue un ejemplo de una gráfica I-MR en excel
6.2 Gráficas de Control para datos discretos o por Atributos
Muchas características de calidad no pueden representarse convenientemente de forma numérica. En estos casos, solemos clasificar cada artículo inspeccionado como producto conforme o producto no conforme con respecto a las especificaciones de calidad.
Los gráficos de atributos no suelen ser tan informativos como los gráficos de variables continuas porque normalmente hay más información en una medición numérica que en la mera clasificación de una unidad como conforme o no conforme.
Sin embargo, los gráficos de atributos tienen aplicaciones importantes. Son especialmente útiles en las industrias de servicios y en los esfuerzos de mejora de la calidad no relacionados con la fabricación porque muchas de las características de calidad que se encuentran en estos entornos no se pueden medir fácilmente en una escala numérica.
6.2.1 Gráficos de control p
Los gráficos P o de fracción de no conformidades se definen como la relación entre el número de artículos no conformes en una población con respecto al número total de artículos de esa población.
Los artículos pueden tener varias características de calidad que son examinadas simultáneamente por el inspector, si el artículo no es conforme o no se ajusta a la especificación de calidad en una o más características, se clasifica como no conforme.
Normalmente expresamos la fracción de no conformidad con un decimal, aunque en ocasiones se utiliza el porcentaje de no conformidad que es simplemente el porcentaje de la fracción no conforme.
Los principios estadísticos en los que se basa el gráfico p o de control de la fracción de no conformidad están basados en la distribución binomial y requerimos cumplir con el principio de independencia (cada unidad producida es independiente de las las unidades que se produjeron en el pasado), y que la muestra se tome sea de manera aleatoria.
Si se selecciona una muestra aleatoria de n unidades de producto, y si D es el número de unidades de producto que no son conformes, entonces D tiene una distribución binomial con parámetros n y p.
La fracción de no conformidad será:
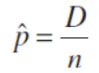
Descargue un ejemplo de una gráfica p en excel
6.2.2 Gráficos de control np
Es posible diseñar un gráfico de control basado en el número de productos no conformes en lugar de la fracción de no conformes. Esto suele denominarse gráfico de control del número de no conformes (np).
Muchas personas que no tienen una formación en estadística encuentran el gráfico np más fácil de interpretar que la fracción no conformidades p.
En este gráfico se calculan los límites de control superior e inferior para que nos den un número entero de no conformidades, así el operador sabrá que si tiene más no conformidades que el límite superior que está dado en unidades el proceso está fuera de control al igual que si el número de no conformidades se encuentra por debajo del límite de control inferior el proceso estará fuera de control.
Se requiere un tamaño de subgrupo constante (n) y dado que los Límites de Control se basan en una aproximación a la normal, el tamaño de muestra usado debiera ser tal que la np ≥ 5.
Nota: En algunos procesos productivos se generan diferentes tamaños de lote en cada uno de los períodos de producción, esta situación nos lleva a que el gráfico de control tenga un tamaño de muestra variable. Hay tres enfoques para construir y operar un gráfico de control con un tamaño de muestra variable sin embargo eso no lo tocaremos en este artículo.
Descargue un ejemplo de una gráfica np en excel
6.2.3 Gráficos de control c
Un artículo no conforme es una unidad de producto que no satisface una o más de las especificaciones para ese producto. Cada punto específico en el que no se satisface una especificación da lugar a un defecto o no conformidad. Por consiguiente, un artículo no conforme contendrá al menos una no conformidad.
Sin embargo, dependiendo de su naturaleza y gravedad, es muy posible que una unidad contenga varias no conformidades y no se clasifique como no conformidad.
Como ejemplo, supongamos que estamos fabricando computadoras personales y cada unidad podría tener uno o varios defectos muy pequeños en el acabado de la carcasa, y dado que estos defectos no afectan gravemente al funcionamiento de la unidad, la unidad se podrían clasificarse como conforme, pero si hay demasiados de estos defectos, la computadora personal se debra clasificar como producto no conforme, ya que tal cantidad de defectos serían muy perceptibles para el cliente y podrían afectar a la venta de la unidad
Hay muchas situaciones prácticas en las que se prefiere trabajar directamente con el número de defectos o no conformidades en lugar de la fracción no conforme.
Por ejemplo, el número de soldaduras defectuosas en 100 m de oleoducto, el número de remaches rotos en el ala de un avión, el número de defectos funcionales en un dispositivo lógico electrónico, el número de errores en un documento, el número de clientes que deciden abandonar un sistema de servicio sin completar su solicitud de servicio, etc.
Es posible desarrollar gráficos de control para el número total de no conformidades en una unidad o el número medio de no conformidades por unidad. Estos gráficos de control suelen suponer que la ocurrencia de no conformidades en muestras son de tamaño constante son modeladas por la distribución de Poisson.
Descargue un ejemplo de una gráfica c en excel
6.2.4 Gráficos de control u
Ahora se puede dar el caso de que no sea factible un tamaño de muestra exactamente igual a una unidad de inspección.
La unidad de inspección se elige para simplificar el funcionamiento o la recolección de datos. Sin embargo, no hay ninguna razón por la que el tamaño de la muestra deba limitarse a una unidad de inspección.
Así pues podríamos establecer un gráfico de control basado en la media o número de no conformidades por unidad de inspección. Si encontramos x no conformidades totales en una muestra de n unidades de inspección, el número medio de no conformidades por unidad de unidad de inspección es:
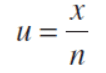
Obsérvese que x es una variable aleatoria de Poisson; en consecuencia, los parámetros del gráfico de control para el número medio de no conformidades por unidad son los siguientes
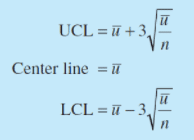
7. CÓMO IMPLEMENTAR EL CONTROL ESTADÍSTICO DE PROCESOS:
La implementación de los gráficos de control o el control estadístico de procesos implica la aplicación de dos fases con dos objetivos distintos.
En la fase I, se recopila un conjunto de datos del proceso (de 25 a 30 muestras por lo general) y se analizan en un análisis retrospectivo, construyendo límites de control de prueba para determinar si el proceso ha estado bajo control durante este periodo de tiempo y con ello ver si se pueden establecer límites de control fiables para supervisar futuros procesos.
Por lo tanto, en la fase I comparamos los m puntos muestreados con los límites de control que son calculados a partir de esos mismos puntos, en la fase I debemos suponer que el proceso está inicialmente fuera de control, por lo que el objetivo es encontrar los puntos que se salen de control e investigar las causas especiales que de ellas deriven para eliminarlas.
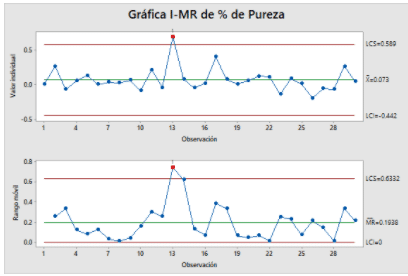
Una vez que se hayan resuelto las causas especiales debemos volver a correr el proceso y recolectar datos para hacer de nuevo el cálculo de los límites de control.
Es importante también verificar que los supuestos de normalidad e independencia y la toma de muestras racionales sean tomados en cuenta.
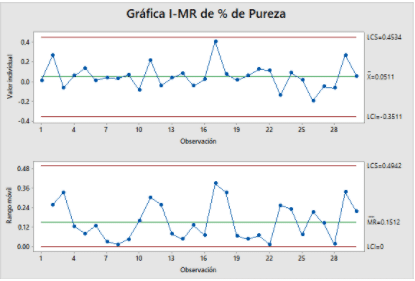
Finalmente, el proceso se estabiliza y se obtiene un conjunto de datos limpios que representan el rendimiento del proceso en control para su uso en la fase II.
En la fase II, el proceso se encuentra en estado estable y utilizamos el gráfico de control para controlar el proceso comparando los datos o muestras con los límites de control, verificando así la estabilidad del proceso en curso
Durante esta fase, el análisis de datos y la reacción a causas especiales se realiza en tiempo real, una vez que el proceso es estable y predecible podemos conocer su capacidad para cumplir de manera consistente con lo que el cliente desea.
8. GRÁFICOS CUSUM Y EWMA
La gráfica de control de sumas acumuladas (cusum) y la gráfica EWMA de promedios móviles con ponderación exponencial son herramientas de control estadístico mucho más poderosas en la fase II que las gráficas tipo Shewhart ya que en caso de que el valor esperado del proceso bajo control se desfase estas gráficas darán la alarma con mayor rapidez.
9. CONCLUSIÓN
Por último, queremos concluir que el Control Estadístico de Procesos (SPC) es una metodología que ayuda a que los procesos trabajen de forma consistente y predecible.
Implementando de forma efectiva el SPC en los procesos de la organización, los productos y/o servicios aumentará la calidad y bajará el costo unitario de fabricación.
El SPC ofrece un lenguaje común para trabajar con el desempeño de los procesos de todas las organizaciones que deciden implementarlo como parte de su estrategia de mejora continua.
10. BIBLIOGRAFÍA
Montgomery, D. C. (2020). Introduction to statistical quality control. Wiley.
Montgomery, D. C. (2013). Statistical quality control: a modern introduction. John Wiley & Sons, Inc.
Ryan, T. P. (2011). Statistical methods for quality improvement. J. Wiley and Sons.
