En este blog, exploraremos de manera sencilla y práctica como calcular la incertidumbre en laboratorios de ensayo.
Esta guía está diseñada para ayudarle a comprender los conceptos clave y aplicarlos de manera efectiva en tus propias mediciones.
Tabla de Contenidos
Toggle¿Qué es la incertidumbre en las mediciones de laboratorio?
La incertidumbre en las mediciones se refiere al rango de valores en el cual se cree que está el valor real de una magnitud medida. En los laboratorios de ensayo, conocer esta incertidumbre es esencial para asegurar la precisión y confianza en los resultados obtenidos.

Importancia de la incertidumbre en los laboratorios de ensayo.
La incertidumbre permite evaluar la fiabilidad de las mediciones realizadas, una información clave para tomar decisiones informadas y cumplir con los estándares de calidad.
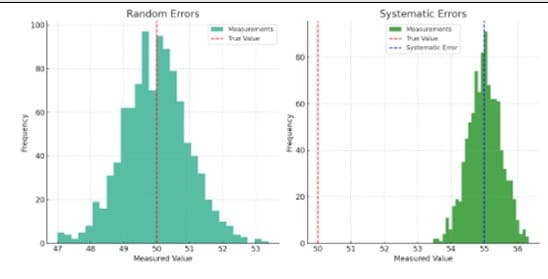
Los errores en las mediciones influyen en el cálculo de la incertidumbre y pueden clasificarse en dos tipos: errores sistemáticos y aleatorios. Reconocer estos errores es esencial para realizar un cálculo adecuado de la incertidumbre.
Tipos de errores que afectan las mediciones: Sistemáticos y Aleatorios.
- Errores Aleatorios o Indeterminados: Estos errores se producen de manera impredecible y suelen deberse a la variabilidad inherente del fenómeno medido o las limitaciones del instrumento. Reducir estos errores es posible mediante mediciones repetidas y métodos estadísticos.
- Errores Sistemáticos o Determinados: Estos errores son constantes y están asociados a factores específicos, como la calibración incorrecta del instrumento o sesgos en el método. Es importante corregirlos para evitar que afecten de forma consistente todas las mediciones.
Evaluación de la incertidumbre estándar en las mediciones.
La desviación estándar, también conocida como incertidumbre estándar y representada como «u» minúscula, es una de las formas más fiables para calcular la incertidumbre, ya que refleja la dispersión de los resultados alrededor del valor promedio, proporcionando así una medida de precisión en los laboratorios de ensayo.
Tipos de evaluación de la incertidumbre: Tipo A y Tipo B.
La incertidumbre en una medición generalmente se compone de diversas fuentes clasificadas en dos tipos:

Evaluación Tipo A:
Basada en el análisis estadístico de observaciones repetidas bajo condiciones similares.
Evaluación Tipo B:
Incluye incertidumbres evaluadas mediante métodos distintos al análisis estadístico, como especificaciones del fabricante o datos previos.
Ambas evaluaciones permiten obtener una estimación completa de la incertidumbre, abarcando tanto la variabilidad aleatoria como contribuciones externas, lo que asegura una comprensión y control precisos de la medición.
Mediciones Directas e Indirectas.
La metodología para evaluar la incertidumbre puede variar según el tipo de medición:
- Mediciones Directas: Se obtienen directamente del instrumento sin necesidad de cálculos adicionales. Ejemplos incluyen medir masa con una balanza o temperatura con un termómetro.
- Mediciones Indirectas: Se obtienen mediante relaciones funcionales o ecuaciones que conectan la magnitud deseada con otras variables medidas directamente, como la densidad calculada a partir de masa y volumen.
Propagación de la incertidumbre y evaluación combinada para mediciones directas.
Para determinar la incertidumbre total en una medición directa, se emplea el método de propagación de incertidumbre. Este método implica sumar cuadráticamente todas las incertidumbres individuales y luego obtener la raíz cuadrada para calcular la incertidumbre estándar combinada.
- Varianza Combinada: Representa la suma de las variancias de cada fuente de incertidumbre.
- Coeficientes de Sensibilidad: Indican cómo el resultado cambia en función de cada variable de entrada, permitiendo evaluar el impacto de cada factor en la incertidumbre combinada.

Pasos básicos para calcular la incertidumbre en el laboratorio (Mediciones directas)
Para calcular la incertidumbre en el laboratorio, sigue estos pasos estructurados:
1. Definir el mensurando (Y): Identificar la magnitud específica a medir.
2. Establecer el modelo físico: Identificar las magnitudes de entrada y el modelo matemático.
3. Identificar las fuentes de incertidumbre: Detectar los factores que introducen variabilidad.
4. Cuantificar cada fuente y asignar una distribución: Determinar la variabilidad de cada fuente y asignar una distribución de probabilidad.
5. Reducir y obtener la incertidumbre estándar: Calcular la incertidumbre estándar de cada fuente.
6. Estimar correlaciones: Evaluar si existen correlaciones entre fuentes de incertidumbre.
7. Calcular la incertidumbre estándar combinada: Usar la propagación de incertidumbre para integrar todas las fuentes.
Ejemplo práctico de cálculo de incertidumbre.
Para ilustrar cómo calcular la incertidumbre en un laboratorio de ensayo, utilizaremos el caso de un laboratorio de pruebas no destructivas que emplea el método de Inspección Visual de acuerdo con la ASME Sec. V Art. 9 Edición 2023.
En este caso, se utiliza una cinta métrica para medir las discontinuidades en las superficies inspeccionadas. Este ejemplo sigue los pasos básicos de la metodología de propagación de incertidumbre y combina las incertidumbres individuales para obtener la incertidumbre expandida.

- Definir el mensurando (Y):
El mensurando es la longitud de las discontinuidades medida con una cinta métrica, con un valor de referencia de 500 mm, tal como se requiere en el estándar ASME para asegurar la precisión de las mediciones. - Establecer el modelo físico y matemático:
- Modelo matemático:
- Magnitud de entrada: Longitud en la escala de la cinta métrica utilizada para medir las discontinuidades en la superficie.
- Modelo matemático:
- Identificar las fuentes de incertidumbre:
- Resolución de la escala: Precisión de la cinta métrica.
- Incertidumbre del equipo: Especificada en el informe del equipo o por el fabricante.
- Repetibilidad de las mediciones: Variabilidad entre mediciones repetidas de la misma discontinuidad.
- Cuantificar la variabilidad de cada fuente y asociarle una distribución:
- Resolución de la escala: La cinta métrica tiene una resolución de 1 mm, asignada con una distribución rectangular. La incertidumbre estándar se calcula como
- Incertidumbre del equipo (U/k): Valor de 0.3 mm, asignado con una distribución normal basada en las especificaciones del fabricante.
- Repetibilidad: Desviación estándar calculada a partir de mediciones repetidas de una misma discontinuidad, con un valor de 0.994 mm y una distribución normal.
- Resolución de la escala: La cinta métrica tiene una resolución de 1 mm, asignada con una distribución rectangular. La incertidumbre estándar se calcula como
- Reducir: Obtener la incertidumbre estándar
:
Elevamos al cuadrado cada componente de incertidumbre y los sumamos para obtener la varianza combinada. Posteriormente, se toma la raíz cuadrada de esta suma para calcular la incertidumbre estándar combinada - Estimar correlaciones:
En este ejemplo, asumimos que no existen correlaciones entre las variables de influencia, por lo que se consideran independientes. - Calcular la incertidumbre estándar combinada
:
La suma cuadrática de cada componente de incertidumbre nos da una incertidumbre estándar combinada de 1.046 mm. - Calcular la incertidumbre expandida:
Aplicando un factor de cobertura (k=2) para lograr un intervalo de confianza del 95%, se obtiene una incertidumbre expandida de 2.093 mm.
Resultado Final: La medición de las discontinuidades en la superficie inspeccionada, realizada con la cinta métrica, tiene una incertidumbre expandida de ±2.0 mm, redondeada a dos cifras significativass. Este valor representa el margen de precisión esperado en las mediciones realizadas bajo el estándar ASME Sec. V Art. 9, Edición 2023, garantizando así la confiabilidad de los resultados obtenidos en el laboratorio de pruebas no destructivas.
Este ejemplo práctico demuestra cómo es posible combinar y evaluar las diferentes fuentes de incertidumbre en una única cifra de incertidumbre combinada y expandida, proporcionando una evaluación confiable que asegura la calidad de las mediciones en contextos de inspección visual de pruebas no destructivas.
Consejos para mejorar la precisión en el cálculo de incertidumbre.

Establecer un procedimiento estándar
Reducir errores con un procedimiento claro asegura resultados consistentes.

Registrar y revisar datos periódicamente
Mantener un registro detallado permite identificar patrones y ajustar métodos.

Calibrar instrumentos regularmente
La calibración regular minimiza los errores sistemáticos y es fundamental para mediciones precisas.
Conclusión
El cálculo de incertidumbre en laboratorios es esencial para asegurar la calidad y precisión en los resultados. Siguiendo una metodología estructurada y aplicando estos pasos, es posible evaluar de manera confiable la incertidumbre y mejorar la precisión de los procedimientos.
Resumen de Pasos Clave
- Definir el mensurando
- Establecer el modelo físico y matemático
- Identificar y cuantificar las fuentes de incertidumbre
- Calcular la incertidumbre estándar combinada
- Expandir la incertidumbre
Importancia de un Cálculo Adecuado
Calcular la incertidumbre de manera precisa permite decisiones informadas y aumenta la confianza en los resultados obtenidos
¿Necesitas Ayuda con el Cálculo de Incertidumbre y la Implementación de la Norma 17025?
Contacta con nosotros para asesoría en Sistemas de Gestión de competencia técnica ISO 17025
¿Necesitas apoyo en la implementación de sistemas de gestión de calidad y en el cálculo de incertidumbre en tu laboratorio?
¡Contáctanos! Estamos aquí para ayudarte a optimizar tus procesos y asegurar la precisión de tus mediciones.
Bibliografía
International Organization for Standardization. (2008). ISO/IEC Guide 98-3:2008. Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM:1995). Geneva: ISO.
American Society of Mechanical Engineers. (2023). ASME Boiler and Pressure Vessel Code, Section V – Nondestructive Examination, Article 9. New York: ASME.
Joint Committee for Guides in Metrology. (2008). Evaluation of measurement data — Guide to the expression of uncertainty in measurement (JCGM 100:2008). BIPM.
Bureau International des Poids et Mesures. (2008). Guide for the Expression of Uncertainty in Measurement (GUM). Retrieved from https://www.bipm.org.
Montgomery, D. C., & Runger, G. C. (2018). Applied statistics and probability for engineers (7th ed.). Wiley.
Taylor, J. R. (1997). An introduction to error analysis: The study of uncertainties in physical measurements (2nd ed.). University Science Books.
Bell, S. (2001). A beginner’s guide to uncertainty of measurement. National Physical Laboratory (NPL). Retrieved from https://www.npl.co.uk.
Centro Nacional de Metrología (CENAM). (n.d.). Evaluación de la incertidumbre en la metrología: Guía para la estimación de la incertidumbre en la medición. Querétaro, México: CENAM.
National Institute of Standards and Technology. (1994). Guidelines for evaluating and expressing the uncertainty of NIST measurement results (NIST Technical Note 1297). Gaithersburg, MD: NIST.
Dieck, R. H. (2007). Measurement uncertainty: Methods and applications (4th ed.). ISA.




